Chain Rule Integration
365 Describe the proof of the chain rule. The chain rule of differentiation of functions in calculus is presented along with several examples and detailed solutions and comments.

Reverse Chain Rule Edexcel A Level Maths Pure Revision Notes

Integration Using The Reverse Of The Chain Rule Worksheet With Solutions A Worksheet On Integration Using The Reverse Of Th Chain Rule Worksheets Solutions
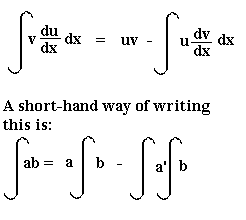
Integration By Parts Mathematics A Level Revision
The more times you apply the chain rule to different problems the easier it becomes to recognize how to apply the rule.
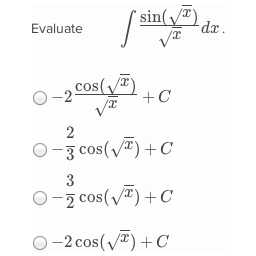
Chain rule integration. For example if a composite function f x is defined as. In calculus the chain rule is a formula that expresses the derivative of the composition of two differentiable functions f and g in terms of the derivatives f and gMore precisely if is the function such that for every x then the chain rule is in Lagranges notation. This section shows how to differentiate the function y 3x 1 2 using the chain rule.
The Chain Rule is a formula for computing the derivative of the composition of two or more functions. 364 Recognize the chain rule for a composition of three or more functions. Chain rule Get 3 of 4 questions to level up.
Players can get started for free and collect NFTs in an ecosystem underpinned by state of the art blockchain technologies. Integration by parts is used to integrate when you have a product multiplication of two functions. Recognize the chain rule for a composition of three or.
The formula of chain rule for the function y fx where fx is a composite function such that x gt is given as. Linear and quadratic approximations. Ses 9-16 complete PDF - 69 MB 10.
361 State the chain rule for the composition of two functions. As you will see throughout the rest of your Calculus courses a great many of derivatives you take will involve the chain rule. Apply the chain rule together with the power rule.
In Chain Rule for One Independent Variable the left-hand side of the formula for the derivative is not a partial derivative but in Chain Rule for Two Independent Variables it is. Interpreting the behavior of accumulation functions. Interpreting the behavior of accumulation functions.
Or equivalently. The chain rule provides us a technique for finding the derivative of composite functions with the number of functions that make up the composition determining how many differentiation steps are necessary. Exponential and Logarithmic functions.
By using this website you agree to our Cookie Policy. There is no general chain rule for integration known. Derivatives of the Trigonometric Functions.
We will also give a nice method for writing down the chain rule for. Let us illustrate it with the help of an example. ChainGuardians is a blockchain game where you can play to earn.
Linearity of the Derivative. Exam 1 review. The Derivative of sin x continued.
If z is a function of y and y is a function of x then the derivative of z with respect to x can be written fracdzdx fracdzdyfracdydx. Finding derivative with fundamental theorem of calculus. The chain rule may also be expressed in Leibniz.
To get chain rules for integration one can take differentiation rules that result in derivatives that contain a composition and integrate this rules once or multiple times and rearrange then. While this is an implementation detail and you should not modify the rules Docker inserts into your iptables policies it does have some implications on what you need to do if you want to have your own policies in addition to those managed by Docker. In a way its very similar to the product rule which allowed you to find the derivative for two multiplied functions.
Iptor is your end-to-end cloud ERP and supply chain partner for a world where exceptions are the rule those make-or-break moments that can unveil a world of opportunities opening new growth paths. Implicit differentiation inverses. The new supply chain rule is to have the required quantity of the right product in the right place at the right time The traditional warehouses are not completely fit to cater to this new supply chain rule and this led to the evolution of static warehouses into distribution centers.
You may abstract a. The rule of first-come first-served will apply. 363 Apply the chain rule and the productquotient rules correctly in combination when both are necessary.
Now it seems the trend may be reversing once more as a definite movementsometimes referred to as Vertical Integration 20gathers momentum. 362 Apply the chain rule together with the power rule. Also in this site Step by Step Calculator to Find Derivatives Using Chain Rule.
The goal of indefinite integration is to get known antiderivatives andor known integrals. Horizontal integration has become the go-to value chain strategy over the last two or three decades to the point where companies that insisted upon remaining vertical became the outliers in a global field of distributed organisations. In this section we discuss one of the more useful and important differentiation formulas The Chain Rule.
The Derivative of sin x 3. It is the counterpart to the chain rule for differentiation and can loosely be thought of as using the chain rule backwards. State the chain rule for the composition of two functions.
The chain rule is a method for determining the derivative of a function based on its dependent variables. In calculus integration by substitution also known as u-substitution or change of variables is a method for evaluating integrals and antiderivatives. Exam 1 covering Ses 1-7 No Lecture Notes Applications of Differentiation.
This is the standard form of chain rule of differentiation formula. However successful SCM requires cross-functional integration of key business processes within the firm and across the network of firms that comprise the. Apply the chain rule and the productquotient rules correctly in combination when both are necessary.
For instance if f and g are functions then the chain rule expresses the derivative of their composition. For example you would use integration by parts for x lnx or xe 5x. Differentiating using the chain rule usually involves a little intuition.
Free Partial Fractions Integration Calculator - integrate functions using the partial fractions method step by step This website uses cookies to ensure you get the best experience. In the section we extend the idea of the chain rule to functions of several variables. Integration using completing the square and the derivative of.
U and v. With the chain rule in hand we will be able to differentiate a much wider variety of functions. In particular we will see that there are multiple variants to the chain rule here all depending on how many variables our function is dependent on and how each of those variables can in turn be written in terms of different variables.
Chain Rule of Differentiation in Calculus. On Linux Docker manipulates iptables rules to provide network isolation. The reason is that in Chain Rule for One Independent Variable z z is ultimately a function of t t alone whereas in Chain Rule for Two Independent Variables z z is a function of both u and v.
Chain management treat it as a synonym for logistics or as logistics that includes customers and suppliers.

Integration Techniques Part Iii
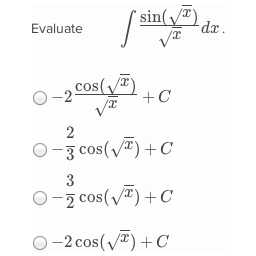
Integration By The Reverse Chain Rule Khan Academy Wiki Fandom

C4 Integration Ppt Download

Integration By Parts Mathematics A Level Revision
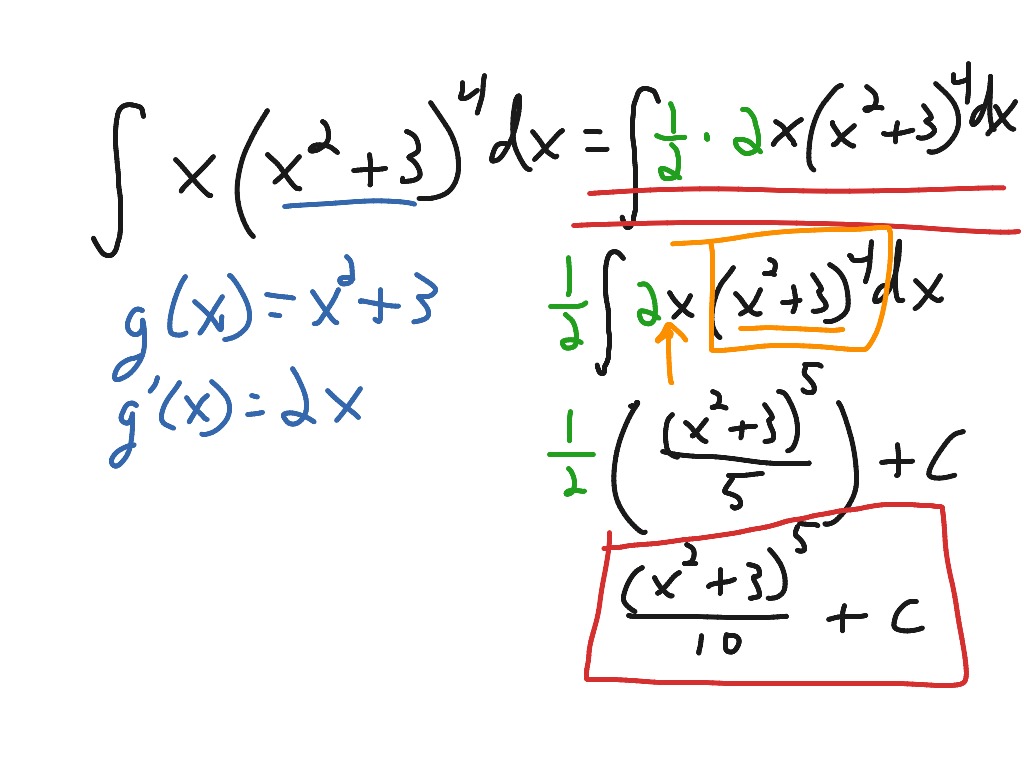
Reverse Chain Rule Practice Math Calculus Integrals Showme
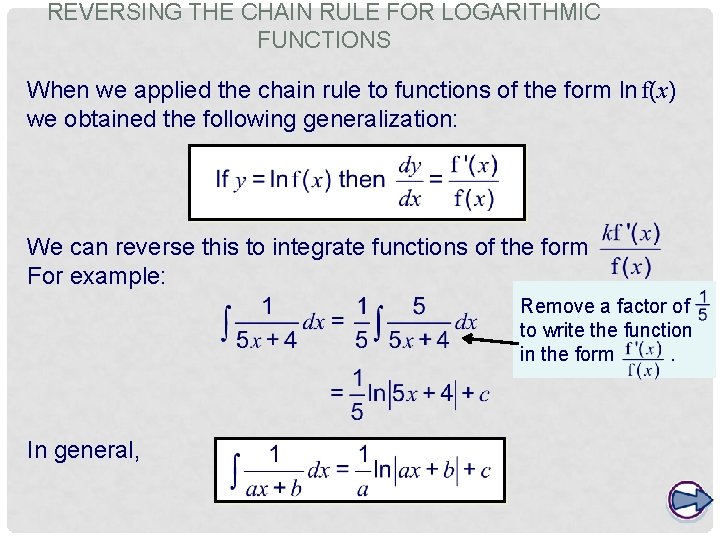
Alevel Maths St 1 Class Integration 1 Integrals

Truly Singaporean Singapore Mathematics H2 Expository Integration By Parts And The D Etail Heuristic

Alevel Maths Core 4 For Edexcel C 4
0 Response to "Chain Rule Integration"
Post a Comment